Jingwen Zheng
  • Mar 26, 2019

Resume of Gradient Descent algorithm

In this blog, I resumed characteristics of 3 different Gradient Descent algorithms: Batch Gradient Descent computes the gradients based on the full training set, it takes long time; Stochastic Grad...

Gradient Descent is a very generic optimization algorithm capable of finding optimal solutions to a wide range of problems. The general idea of Gradient Descent is to tweak parameters iteratively so that we can minimize a cost function. An important parameter in Gradient Descent is the size of the steps, determined by the learning rate hyperparameter. In this blog, I will talk about how to determine the the size of the steps in different case with following models:

  • Batch Gradient Descent
  • Stochastic Gradient Descent
  • Mini-batch Gradient Descent
  • Comparison

Batch Gradient Descent

To implement Gradient Descent, you need to compute the gradient of the cost function with regards to each model theta_j. This is called a partial derivative.

Partial derivatives of the cost function:

BGD partial derivatives of the cost function

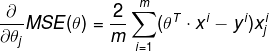
Notice that this formula involves calculations over the full training set X, at each Gradient Descent step! That is why the algorithm is called Batch Gradient Descent: it uses the whole batch of training data at every step.

Stochastic Gradient Descent

The main problem with Batch Gradient Descent is the that is uses the whole training set to compute the gradients at every step, which makes it very slow when the training set is large. At the opposite extreme, Stochastic Gradient Descent just picks a random instance in the training set at each step and computes the gradients based only on the single instance.

Randomness is good to escape from local optima, but bad since it means that the algorithm can never settle at the minimum. One solution is to gradually reduce the learning rate. The steps start out large, then get smaller and smaller, allowing the algorithm to settle at the global minimum. However, if you want to be sure that the algorithm goes through every instance at each epoch, another approach is to shuffle the training set, go through it instance by instance, then shuffle it again, and so on.

To perform Linear Regression using SGD with Scikit-Learn, we can use the SGDRegressor class, which defaults to optimizing the squared error cost function.

import numpy as np
from sklearn.linear_model import SGDRegressor

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)

# 50 epochs, learning rate = 0.1
sgd_reg = SGDRegressor(n_iter=50, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
# (array([4.16782089]), array([2.72603052]))

The code above runs 50 epochs, starting with a learning rate of 0.1, using the default learning schedule and it doesn’t use any regularization.

Mini-batch Gradient Descent

Once you know Batch Gradient Descent and Stochastic Gradient Descent, it’s really simple to understand Mini-batch Gradient Descent: at each step, instead of computing the gradients based on the full training (like Batch Gradient Descent) set or based on just one instance (like Stochastic Gradient Descent), Mini-batch Gradient Descent computes the gradients on small random sets of instances called mini-batches. The main advantage of Mini-batch Gradient Descent is that you can get a performance boost from hardware optimization of matrix operations.

Comparison

Let’s compare the algorithms we’ve discussed, m is the number of training instances, n is the number of features.

Algorithm Large m Out-of-core support Large n Hyperparams Scaling required Scikit-Learn class
Normal Equation Fast No Slow 0 No LinearRegression
Batch GD Slow No Fast 2 Yes n/a
Stochastic GD Fast Yes Fast >= 2 Yes SGDRegressor
Mini-batch GD Fast Yes Fast >= 2 Yes SGDRegressor

Conclusion

In this blog, I resumed characteristics of 3 different Gradient Descent algorithms: Batch Gradient Descent computes the gradients based on the full training set, it takes long time; Stochastic Gradient Descent picks just one instance of training set, it has a better chance of finding the global minimum than Batch GD; Mini-batch Gradient Descent computes the gradients on small random sets of instances, it get a performance boost from hardware optimization of matrix operations. Hope it’s useful for you.

Reference

Search