Jingwen Zheng
  • Apr 02, 2019

Resume of Regularized Linear Models

A good way to reduce overfitting is to regularize the model, which means the fewer degrees of freedom it has, the harder it will be for it to overfit the data. For a linear model, regularization is...

A good way to reduce overfitting is to regularize the model, which means the fewer degrees of freedom it has, the harder it will be for it to overfit the data. For a linear model, regularization is achieved by constraining the weights of the model. In this blog, I will talk about how to constrain the weights of the following models:

  • Ridge Regression
  • Lasso Regression
  • Elastic Net

Ridge Regression

Ridge Regression is a regularized version of Linear Regression: a regularization term reg term is added to the cost function. Note that the regularization term should only be added to the cost function during training.

The hyperparameter α controls how much you want to regularize the model. If α = 0, then Ridge Regression is Linear Regression. If α is pretty large, then all weights end up very close to zero and the result is a flat line going through the data’s mean.

Ridge Regression cost function:

Ridge Regression cost function

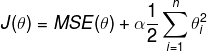
We can define w as the vector of feature weights, then the regularization term is equal to l2 norm, where l2 norm label represents the l2 norm of the weight vector.

Here is how to perform Ridge Regression with scikit-learn:

import numpy as np
from sklearn.linear_model import Ridge

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.rand(100, 1)
ridge_reg = Ridge(alpha=1, solver='cholesky')
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
# array([[5.58066253]])

Lasso Regression

Least Absolute Shrinkage and Selection Operator Regression (simply called Lasso Regression) is another regularized version of Linear Regression, it adds a regularization term to the cost function, but uses the l1 norm of the weight vector instead of half the square of the l2 norm.

Lasso Regression cost function:

Lasso Regression cost function

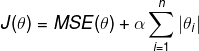
An important characteristic of lasso Regression is that it tends to completely eliminate the weights of the least important features.

Here is how to perform Lasso Regression with scikit-learn:

from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
# array([5.53996101])

Elastic Net

Elastic Net is a middle ground between Ridge Regression and Lasso Regression. The regularization term is a simple mix of theirs, we can also control the mix ratio r. When r = 0, Elastic Net is Ridge Regression; when r = 1, Elastic Net is Lasso Regression.

Elastic Net cost function:

Elastic Net cost function

Here is how to perform Lasso Regression with scikit-learn:

from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
# array([5.53792412])

Conclusion

So when should we use Linear Regression, Ridge Regression, Lasso Regression or Elastic Net?

It’s almost always preferable to have at least a little bit of regularization, so we should avoid plain Linear Regression. Ridge Regression is a good choice by default. However, if you suspect that only a few features are useful, you should choose Lasso Regression or Elastic Net, because they tend to completely eliminate the weights of the least important features. If the number of features is greater than the number of training instances or if several features are strongly correlated, Elastic Net is preferred over Lasso Regression since Lasso may behave erratically.

Reference

Search