Jingwen Zheng
  • Apr 16, 2019

Resume of Logistic & Softmax Regression

In this blog, I will resume Logistic Regression, Softmax Regression and their usecases via Python.

In this blog, I will talk about two models that are commonly used for classification tasks: Logistic Regression and Softmax Regression.

Logistic Regression

Logistic Regression is commonly used to estimate the probability that an instance belongs to a particular class. It’s a binary classifier. Like a Linear Regression model, a Logistic Regression model computes a weighted sum of the input features, but instead of outputting the result like the Linear Regression does, it outputs the logistic of the result (like the following equation).

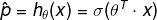
Logistic Regression model estimated probability

The objective of training is to set the parameter vector θ so that the model estimates high probabilites for positive instances and low probabilities for negative instances. This idea is captured by the following cost function:

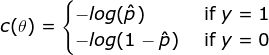
Logistic Regression cost function

This function makes sense since -log(t) grows very large if t approaches 0, so the cost will be large if the model estimates a probability close to 0 for a positive instance; and it will also be very large if the model etimates a probability close to 1 for a negative instance.

Demo

Let’s use the iris dataset and try to build a classifier to detect the Iris-Virginica type based only on the petal width feature.

>>> from sklearn import datasets
>>> import numpy as np

>>> iris = datasets.load_iris()
>>> list(iris.keys())
['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']
>>> X = iris['data'][:, 3:] # petal width
>>> y = (iris['target'] == 2).astype(np.int)

>>> from sklearn.linear_model import LogisticRegression
>>> log_reg = LogisticRegression()
>>> log_reg.fit(X, y)
>>> log_reg.predict([[1.7], [1.5]])
array([1, 0])

The classifier predicts that if a flower’spetal width is 1.7 cm, then it’s an Iris-Virginica; if a flower’spetal width is 1.5 cm, then it is not an Iris-Virginica.

Softmax Regression

The Logistic Regression model can be generalized to support multiple classes directly, without having to train and combine multiple binary classifiers. This is called Softmax Regression, or Multinomial Logistic Regression.

How it works? When given an instance x, the Softmax Regression model first computes a score s_k(x) for each class k, then estimates the probability of each class by applying the softmax function to the scores.

Softmax score for class k:

Softmax score for class k

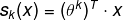
Note that each class has its owm dedicated parameter vector theta^k. Once you have computed the score of each class for the insrance x, you can estimate the probability p^hat_k that the instance belongs to class k by running the scores through the softmax function (as follows): it computes the exponential of every score, then normalizes them.

Softmax function:

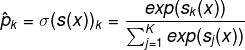
Softmax function

The objective is to have a model that estimates a high probability for the target class. Minimizing the cost function called cross entropy should lead to this objective since it penalizes the odel whenit estimates a low probability for a target class. Cross entropy is frequentyly used to measure how well a set of estimated class probabilities match the target classes.

Cross entropy cost function:

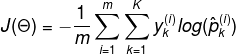
Cross entropy cost function

y_k^i is equal to 1 if the target class for the ith instance is k; otherwise, it’s equal to 0.

Notice that when K=2, the cost function is equivalent to the Logistic Regression’s cost function.

Demo

Let’s use Softmax Regression to classify the iris flowers into all three classes.

>>> X = iris['data'][:, (2, 3)]
>>> y = iris['target']
>>> softmax_reg = LogisticRegression(multi_class='multinomial', # switch to Softmax Regression
                                     solver='lbfgs', # handle multinomial loss, L2 penalty
                                     C=10)
>>> softmax_reg.fit(X, y)

>>> softmax_reg.predict([[5, 2]])
array([2])
>>> softmax_reg.predict_proba([[5, 2]])
array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])

If a flower’s petal length is 5 cm and its petal width is 2 cm, it is an Iris-Virginica with 94.2% probability.

Conclusion

In this blog, I resumed Logistic Regression, Softmax Regression and their usecases via Python. Hope it’s useful for you.

Reference

Search